Linear Programming
Operations management often presents complex problems that can be modeled by linear functions. The mathematical technique of linear programming is instrumental in solving a wide range of operations management problems.
Linear Program Structure
Linear programming models consist of an objective function and the constraints on that function. A linear programming model takes the following form:
Objective function:
Z = a1X1 + a2X2 + a3X3 + . . . + anXn
Constraints:
b11X1 + b12X2 + b13X3 + . . . + b1nXn <>1
b21X1 + b22X2 + b23X3 + . . . + b2nXn <>2
.
.
.
bm1X1 + bm2X2 + bm3X3 + . . . + bmnXn <>m
In this system of linear equations, Z is the objective function value that is being optimized, Xi are the decision variables whose optimal values are to be found, and ai, bij, and ci are constants derived from the specifics of the problem.
Linear Programming Assumptions
Linear programming requires linearity in the equations as shown in the above structure. In a linear equation, each decision variable is multiplied by a constant coefficient with no multiplying between decision variables and no nonlinear functions such as logarithms. Linearity requires the following assumptions:
Proportionality - a change in a variable results in a proportionate change in that variable's contribution to the value of the function.
Additivity - the function value is the sum of the contributions of each term.
Divisibility - the decision variables can be divided into non-integer values, taking on fractional values. Integer programming techniques can be used if the divisibility assumption does not hold.
In addition to these linearity assumptions, linear programming assumes certainty; that is, that the coefficients are known and constant.
Problem Formulation
With computers able to solve linear programming problems with ease, the challenge is in problem formulation - translating the problem statement into a system of linear equations to be solved by computer. The information required to write the objective function is derived from the problem statement. The problem is formulated from the problem statement as follows:
Identify the objective of the problem; that is, which quantity is to be optimized. For example, one may seek to maximize profit.
Identify the decision variables and the constraints on them. For example, production quantities and production limits may serve as decision variables and constraints.
Write the objective function and constraints in terms of the decision variables, using information from the problem statement to determine the proper coefficient for each term. Discard any unnecessary information.
Add any implicit constraints, such as non-negative restrictions.
Arrange the system of equations in a consistent form suitable for solving by computer. For example, place all variables on the left side of their equations and list them in the order of their subscripts.
The following guidelines help to reduce the risk of errors in problem formulation:
Be sure to consider any initial conditions.
Make sure that each variable in the objective function appears at least once in the constraints.
Consider constraints that might not be specified explicitly. For example, if there are physical quantities that must be non-negative, then these constraints must be included in the formulation.
The Effect of Constraints
Constraints exist because certain limitations restrict the range of a variable's possible values. A constraint is considered to be binding if changing it also changes the optimal solution. Less severe constraints that do not affect the optimal solution are non-binding.
Tightening a binding constraint can only worsen the objective function value, and loosening a binding constraint can only improve the objective function value. As such, once an optimal solution is found, managers can seek to improve that solution by finding ways to relax binding constraints.
Shadow Price
The shadow price for a constraint is the amount that the objective function value changes per unit change in the constraint. Since constraints often are determined by resources, a comparison of the shadow prices of each constraint provides valuable insight into the most effective place to apply additional resources in order to achieve the best improvement in the objective function value.
The reported shadow price is valid up to the allowable increase or allowable decrease in the constraint.
Applications of Linear Programming
Linear programming is used to solve problems in many aspects of business administration including:
- product mix planning
- distribution networks
- truck routing
- staff scheduling
- financial portfolios
- corporate restructuring
Operations > Linear Programming
LINEAR PROGRAMMING
D.W. Ellis & Associates Ltd.
2220 142 Ave. Edmonton, Alta. T5Y 1E6 Canada - (780) 457-7491 - email David Ellis
A Competitive Advantage for Planning and Productivity
This information on Linear Programming is designed to be read sequentially. You can, however, go directly to any of the following sections:
- Introduction to Linear Programming
- Example Linear Programming Model
- Example Linear Programming Uses
- Our Services
- Our Experience
- D.W. Ellis & Associates Ltd.
INTRODUCTION TO LINEAR PROGRAMMING
Linear Programming is a method of expressing and optimizing a business problem with a mathematical model. It is one of the most powerful and widespread business optimization tools.
To a person with no background in the management sciences, it may be hard to believe but the tool, linear programming, can be used in a very large variety of business problems. They include:
- transportation distribution problems
- production scheduling in oil & gas, manufacturing, chemical, etc industries
- financial and tax planning
- human resource planning
- facility planning
- fleet scheduling
LINEAR PROGRAMMING; an optimization technique capable of solving an amazingly large variety of business problems. A business objective (e.g. minimize costs of a distribution system), business restrictions (storage capabilities, transportation volume restrictions), and costs/revenue (storage costs, transportation costs) are formulated into a mathematical model. Algorithms for finding the best solutions are used. For more details on linear programming see the section below.
To properly apply linear programming, the analyst must be not only an expert in the tool but also have experience with the particular business situation. In this regard, a team on the project whose members represent expertise in linear programming and in the business expertise work very well.
Some other descriptions of linear programming available on the web are:
EXAMPLE LINEAR PROGRAMMING MODEL
An introductory text on management science or operations research will contain a section on linear programming. The following is an example problem.
A company makes 2 kinds of cement at its plant. It can also purchase these 2 kinds of cement at a different location. As well, it maintains 4 storage locations where it ships product for subsequent delivery to customers. It can also ship cement directly from its plant or point of purchase. It has many customs at various locations. How much of each kind of cement should it produce or purchase? What storages should be supplied from the plant and which from the point of purchase? What customers should be supplied from each of the 6 supply points? This is a large problem and its solution can make the difference between success and failure of the company.
To solve this problem, we need to formulate it as a linear program. Some notation is needed. Let i = 1 to 6 be the 6 points of shipment (the plant, the point of purchase and the 4 storages). Let j = 1 to n be the customers. Let k= 1 to 2 be the products.
Let xa(k) be the amount of product k made at the plant, xb(k) the amount of product k purchased, ta(i=1,2;i=3,6;k) be the amount of product k shipped from the plant and the point of purchase (i=1,2) to the 4 storage locations (i=3,6), and tb(i,j,k) be the amount of product k shipped from the 6 storage locations (i) to the n customers (j).
Let m(k) be the cost of making the product k at the plant, p(k) be the cost of purchasing the product k at the point of purchase, d(i=1,2;i=3,6) be the cost of sending product from the plant or point of purchase (i=1,2) to the 4 storage locations (i=3,6), and c(i,j) be the cost of sending product from the 6 points of shipment to each of the n customers (it is the same for each product).
Let M(k) be the maximum amount of product k that can be made at the plant, P(k) be the maximum amount of product k that can be purchased, and D(j,k) the demand by customer j for product k.
The real business issues that would be included in a full linear programming implementation of this problem include multiple time periods, delivery timing, costs that change with volume, handling situations when all customer demand cannot be met.
The formulation includes a cost objective function to be minimized:
2 2 2 6 2 6 n 2
[ m(k)xa(k) + [p(k)xb(k) + [ [d(i=1,2;i=3,6) [ta(i=1,2;i=3,6;k) + [ [c(i,j) [tb(i,j,k)
k=1 k=1 i=1 i=3 k=1 i=1 j=1 k=1
The constraints on the solution require that the limits be met:
limit on the amount produced
xa(k) <= M(k) for k=1,2
limit on the amount purchased
xb(k) <= P(k) for k=1,2
meet customer demand
6
[tb(i,j,k) = D(j,k) for j=1,n and k=1,2
i=1
Existing software would quickly find the optimal solution.
The model should be complex enough to include all of the true details of the situation.
EXAMPLE LINEAR PROGRAMMING USES
- Production planning in a chemical plant. This model optimized the operation of each unit and the use of storage facilities to meet demand at least cost.
- Refinery scheduling. Similar to the above but more than one location was involved and distribution to the customers was included.
- Rail fleet optimization. The model decided on the rail car leases for 3 types (heated, insulated, normal) of rail cars to minimize the cost of distributing product throughout Canada. Seasonal variations and car movement across the country were included.
- Truck fleet utilization. Given a fleet of trucks of different sizes and operating characteristics and costs, this model decided what trucks should be used for what deliveries from a distribution terminal to customers.
- Truck designs. The axle spacing on trucks are subject to complex loading rules. In some provinces, the design of these axle spacings can be modeled using linear programming to maximize load.
- Tax model. Personal and corporate taxes can be minimized using a linear programming model. It includes the best mix of dividends and salaries and the progressive personal tax rates.
- Oil and Gas production planning. This model optimized the actual production and the allocation of production to contracts to minimize costs to the producer.
- 'Take or Pay' optimization. Formerly gas contracts in Alberta included minimum volume purchases. In low demand periods, the purchaser had to decide from which contracts to pay for gas even though it was not delivered. Complicated payment schemes and recoveries were included.
- Off site storage locations were determined through case studies using an integer linear programming model. The entire product storage and delivery plan was optimized for various configurations of locations for the off site storage locations in order to select the best set of these storage locations.
OUR SERVICES
D.W. Ellis & Associates Ltd., with 28 years of experience, offers a complete consulting service in the Management Sciences. For our clients, this means being close to your business, knowing your business, and unmatched responsiveness and costs. We have worked with many large and small Alberta and national companies to simulate various aspects of their business.
Our services revolve around 6 main phases of model development:
- Feasibility Study
- Model Specification Development
- Model Development
- Implementation
- Client Training
- Validation
Feasibility Study
This short study (1-3 weeks) allows the client to obtain a detailed look at what the model will be able to do, the costs and the timing. The client's decision to continue is required at this point.
Model Specification Development
This phase requires significant time on the client's part. The client must provide the modeler with details of his business situation. Included is the level of detail to be modeled, the extent of the process to be modeled, and the format of the input data and reports produced.
Model Development
D.W. Ellis & Associates Ltd. will be responsible for this phase. The client will be provided with intermediate results so progress can be monitored and changes can be made as they are required.
Implementation
This phase is usually very short. The model is transferred to the client's computer and tested. As only PC's are involved, there are typically few complications.
Client Training
Although the client will be involved as the model is designed and developed, additional training on the use of the model will be included in the plan. The client will have been involved with the details of the input data and the reports produced. An organized approach to case analysis and the interpretation of the data will be covered.
Validation
The client must select a typical period of historical time, and collect the data for this time period, and the model is run. Its results are compared to the known results for this period. The model and the data are adjusted to obtain a very close fit between the model results and the known results. The model is now ready for extensive case studies.
EXPERIENCE
Industries with whom D.W. Ellis and Associates Ltd. has consulted concerning facilities or operations modeling:
- Government
- Oil and Gas
- Chemical
- Mining (including the oil sands/tarsands)
- Steel
- Pipeline
- School Boards
- Transit Properties
- Cement Production and Distribution
- Aluminum Production
| Linear Programming | |
Linear programming, sometimes known as linear optimization, is the problem of maximizing or minimizing a linear function over a convex polyhedron specified by linear and non-negativity constraints. Simplistically, linear programming is the optimization of an outcome based on some set of constraints using a linear mathematical model.
Linear programming is implemented in Mathematica as LinearProgramming[c, m, b], which finds a vector ![]() which minimizes the quantity
which minimizes the quantity ![]() subject to the constraints
subject to the constraints 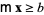 =b" width="44" border="0" height="14"> and
=b" width="44" border="0" height="14"> and 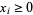 =0" width="33" border="0" height="16"> for
=0" width="33" border="0" height="16"> for ![]() .
.
Linear programming theory falls within convex optimization theory and is also considered to be an important part of operations research. Linear programming is extensively used in business and economics, but may also be used to solve certain engineering problems.
Examples from economics include Leontief's input-output model, the determination of shadow prices, etc., an example of a business application would be maximizing profit in a factory that manufactures a number of different products from the same raw material using the same resources, and example engineering applications include Chebyshev approximation and the design of structures (e.g., limit analysis of a planar truss).
Linear programming can be solved using the simplex method (Wood and Dantzig 1949, Dantzig 1949) which runs along polytope edges of the visualization solid to find the best answer. Khachian (1979) found a ![]() polynomial time algorithm. A much more efficient polynomial time algorithm was found by Karmarkar (1984). This method goes through the middle of the solid (making it a so-called interior point method), and then transforms and warps. Arguably, interior point methods were known as early as the 1960s in the form of the barrier function methods, but the media hype accompanying Karmarkar's announcement led to these methods receiving a great deal of attention.
polynomial time algorithm. A much more efficient polynomial time algorithm was found by Karmarkar (1984). This method goes through the middle of the solid (making it a so-called interior point method), and then transforms and warps. Arguably, interior point methods were known as early as the 1960s in the form of the barrier function methods, but the media hype accompanying Karmarkar's announcement led to these methods receiving a great deal of attention.
Linear programming in which variables may take on integer values only is known as integer programming.
In the Season 4 opening episode "Trust Metric" (2007) of the television crime drama NUMB3RS, math genius Charlie Eppes uses the phrase "you don't need Karmarkar's algorithm" to mean "you don't need to be a rocket scientist to know...."
Using Linear Programming to Predict Business Failure
An Empirical Study
Jan Wallin and Stefan Sundgren 1995
This paper was originally published in Liiketaloudellinen aikakausikirja (1995).
Table of Contents
Abstract
Mathematical programming has been suggested by several authors as a method for discriminant analysis. Most of the studies published to date focus on the technical development of the method, whereas empirical testing has received very little attention. The present study aims at testing one of the basic model formulations on a large sample of firms, the task being to predict business failure. Our findings suggest that the mathematical programming model performs at least as well as logistic regression.
Introduction
Articles proposing mathematical programming (MP) as a method for discriminant analysis have appeared at irregular intervals in scientific journals for more than twenty years. Grinold [6], who in the early 1970s formulated several model variations for pattern classification and cluster analysis, is one of the pioneers. Freed and Glover [2, 3] revived interest in this field in the early 1980s, and judging from the list of references in, e.g., Ragsdale and Stam [8] a strong interest among many researchers survived through the 1980s into the early 1990s.
What interests most researchers is the fact that under certain circumstances some model formulations are afflicted by a propensity for degeneracy and instability. Most of these problems have to do with how the weights of the estimated function are normalized. Several remedies have been suggested. In this study we choose a simple normalization procedure in the form of a constraint that is added to the basic Freed-Glover model. The procedure was employed as early as 1974 by, among others, Pekelman and Sen [7] in a study of brand choice. This was proposed much later later by (Freed and Glover [4]). Several other suggestions have been made later in the literature (among others, Glover [5]; Ragsdale and Stam [8]); Rubin [9], but since these complicate computations substantially, and since we feel that the earlier suggestions have not been sufficiently tested, we focus on the one mentioned above. What this entails in detail will be described in the next section.
Apart from problems of a technical nature, there may also be a problem of inferior performance. One of the few empirical tests that have been carried out suggests that the performance of the original Freed-Glover model does not seem to be as good as that of statistical techniques such as logistic regression (logit) and sequential partitioning (Srinivasan and Kim [10]). Several ways to improve the performance of the model have been suggested in recent years (among others, Glover [5]; Ragsdale and Stam [8]). The problem with these suggestions is that they also substantially increase the number of computations, which reduces the practical usefulness of the method. The rationale for developing MP models for the discriminant problem was initally that the models were very simple. Since there already exist complicated statistical techniques that function well, one could seriously question the need for developing alternative models that do not have the advantage of being simple and easy to use. This is the main reason why we choose to focus on an augmented version of the basic Freed-Glover model. An additional reason is that we feel that the original version of this model has not been adequately tested. As Eisenbeis [1] has pointed out, the sample Srinivasan and Kim used was rather small, which makes it premature to draw any firm conclusions about the empirical performance of the method.
The present study aims at cross-validating the estimated discriminant function on a large sample of Finnish firms and comparing it with a logit function in a bankruptcy prediction setting, the hypothesis being that the predictive ability of the MP model is at least as good as that of the logit model estimated with the aid of the default version of the BMDP program LR.
The Mathematical Programming Model
The MP model to be tested in this study aims at classifying firms into two categories, failed and non-failed ones, by finding a breakpoint for the weighted sum of a set of financial ratios. The weights are also unknown and will be determined by the model. In the case of binary classification, the ideal situation is that the weighted sums of financial ratios representing non-failed firms are higher than the breakpoint, whereas the sums representing failed firms are lower than this. In practice, however, the situation is not this clear-cut: there may be some failed firms that perform better in terms of the selected ratios than some non-failed firms. This means that the weighted sums of the ratios can be higher for some failed firms than the breakpoint, and vice versa for some non-failed firms. The objective is then to determine the breakpoint and the weights so that these violations of the ideal situation will be minimized.

The last constraint, which sets the sum of the weights to 1, is used to normalize the raw scores of the ratios and to prevent a degenerate solution in which all weights are equal to zero. This constraint was used by Pekelman and Sen [7] in a model of brand preference expressed in pairwise comparisons. This is also one of the suggestions Freed and Glover make in [4]. In the original Freed-Glover model the breakpoint B was treated as a constant which could result in a degenerate solution.
Data
Since financial ratios representing profitability, liquidity and leverage have often turned out to be good predictors of bankruptcy, we decided to limit the selection of ratios to one per category. The selected ratios are: (1) net income plus depreciation/total assets (NIPDTA), (2) quick assets less current liabilities/total assets (QALCLTA), and (3) total debts/total assets (TDTA). Since the third ratio can be expected to be higher for failed firms than for non-failed firms, the weight of this ratio can be expected to be negative. The logit model can handle this automatically, but not the MP model; all unknown variables in the latter type of model must be non-negative. Instead of TDTA we therefore used its inverse, named TATD.
The Central Statistical Office of Finland (CSOF) supplied us with data for the study. The ratios were calculated based on unadjusted financial statement data and stored on a floppy disc. Generally, it may be desirable to adjust raw data, but since we are interested in a comparison of two competing methods, this should not be a problem.
Focusing our attention solely on the manufacturing industry, we used a sample of matched pairs to estimate the discriminant functions, a procedure that is common and economical. Since there were very few failed firms in the CSOF database for a particular year, we decided to include firms that went bankrupt in 1986, 1987, 1988 and 1989. In this manner we obtained 55 failed firms. Adding 55 randomly selected non-failed firms for fiscal 1986 resulted in an estimation sample comprising 110 firms. The estimated weigths and breakpoints are shown in Table 1.
Table 1. Estimated weights and breakpoints.
MP Logit
Constant -5.228
NIPDTA 0.86275 17.460
QALCLTA 0.06180
TATD 0.07545 3.646
Breakpoint 0.11815 0.458
As can be seen, the logit model includes two ratios only: the profitability ratio, NIPDTA, and the leverage ratio, TATD, whereas the MP model includes all of the three ratios used as input variables: NIPDTA, QALCLTA and TATD. The breakpoint for the logit model was set to 0.458 because this value minimized both the number of misclassified failed firms and misclassified non-failed firms in the estimation sample.
Cross-Validation
The estimated discriminant functions were cross-validated on data for fiscal 1987. We wanted the holdout sample to be large and the proportion between failed and non-failed firms to be an approximation of the proportion in the population. This resulted in a holdout sample comprising 1,000 firms, 78 of which failed in 1987, 1988, 1989 and 1990. Thus, the task was to predict bankruptcy within three years or less. This means that the models were subjected to a severe test, especially since 1990 marks the onset of a deep recession in Finland.
The classification rule used for the purpose of cross-validation was the following: If the weighted sum (or the logit probability of success) was greater than the breakpoint, then the firm was classified as a non-failed firm, otherwise it was classified as a failed firm. The results of the comparison of the estimated discriminant functions are shown in Table 2.
Table 2. Results of the predictive test.
Failed firms Number
classified by both
methods
as failed 51
as non-failed 20
classified
differently
MP: failed; 6
logit: non-failed
MP: non-failed; 1
logit: failed
Total 78
Non-failed firms
classified by both
methods
as non-failed 673
as failed 214
classified
differently
MP:non-failed; 22
logit: failed
MP:failed; 13
logit: non-failed
Total 922
As can be seen, application of the MP discriminant function resulted in fewer misclassified failed firms (6-1=5) as well as fewer misclassified non-failed firms (22-13=9). Translated into an ordinary classification table, the results are as shown in Table 3. A comparison is also made with classification results from the estimation sample.
Table 3. Percentages of misclassified firms.
Estimation Holdout
sample sample
MP Logit MP Logit
Failed firms 23.6% 21.8% 26.9% 33.3%
Non-failed firms 21.8% 16.4% 24.6% 25.6%
Total 22.7% 19.1% 24.8% 26.2%
Mathematical approach to the problem of allocating limited resources among competing activities in an optimal manner. Specifically, it is a technique used to maximize revenue, Contribution Margin (CM) or profit function or to minimize a cost function, subject to constraints. Linear programming consists of two important ingredients: (1) objective function and (2) constraints, both of which are linear. In formulating the LP problem, the first step is to define the decision variables that one is trying to solve. The next step is to formulate the objective function and constraints in terms of these decision variables. For example, assume a firm produces two products, A and B. Both products require time in two processing departments, assembly and finishing. Data on the two products are as follows:

The firm wants to find the most profitable mix of these products. First, define the decision variables as follows:
A = the number of units of product A to be produced
B = the number of units of product B to be produced
Then, express the objective function, which is to maximize total contribution margin (TCM), as:
TCM = $25A + $40B
Formulate the constraints as inequalities:
2A + 4B < 100
3A + 2B < 90
and do not forget to add the non-negative constraints:
A > 0, B > 0
| C & C++ Jobs for Freshers 1000's of Jobs in C & C++. Submit your Resume Free Now. MonsterIndia.com |
| C++ Imagine Finding Your Dream Job At The Touch Of A Button. Do It Now! www.TimesJobs.com |
| Britannica Concise Encyclopedia: linear programming |
For more information on linear programming, visit Britannica.com.
| Columbia Encyclopedia: linear programming |
| Wikipedia: Linear programming |
In mathematics, linear programming (LP) is a technique for optimization of a linear objective function, subject to linear equality and linear inequality constraints. Informally, linear programming determines the way to achieve the best outcome (such as maximum profit or lowest cost) in a given mathematical model given some list of requirements represented as linear equations.
More formally, given a polytope (for example, a polygon or a polyhedron), and a real-valued affine function
defined on this polytope, a linear programming method will find a point in the polytope where this function has the smallest (or largest) value. Such points may not exist, but if they do, searching through the polytope vertices is guaranteed to find at least one of them.
Linear programs are problems that can be expressed in canonical form:
- Maximize

- Subject to

 represents the vector of variables (to be determined), while
represents the vector of variables (to be determined), while  and
and  are vectors of (known) coefficients and
are vectors of (known) coefficients and  is a (known) matrix of coefficients. The expression to be maximized or minimized is called the objective function (
is a (known) matrix of coefficients. The expression to be maximized or minimized is called the objective function ( in this case). The equations
in this case). The equations  are the constraints which specify a convex polyhedron over which the objective function is to be optimized.
are the constraints which specify a convex polyhedron over which the objective function is to be optimized.
Linear programming can be applied to various fields of study. Most extensively it is used in business and economic situations, but can also be utilized for some engineering problems. Some industries that use linear programming models include transportation, energy, telecommunications, and manufacturing. It has proved useful in modeling diverse types of problems in planning, routing, scheduling, assignment, and design.
History of linear programming
The problem of solving a system of linear inequalities dates back at least as far as Fourier, after whom the method of Fourier-Motzkin elimination is named. Linear programming arose as a mathematical model developed during the second world war to plan expenditures and returns in order to reduce costs to the army and increase losses to the enemy. It was kept secret until 1947. Postwar, many industries found its use in their daily planning.
The founders of the subject are Leonid Kantorovich, a Russian mathematician who developed linear programming problems in 1939, George B. Dantzig, who published the simplex method in 1947, John von Neumann, who developed the theory of the duality in the same year. The linear programming problem was first shown to be solvable in polynomial time by Leonid Khachiyan in 1979, but a larger theoretical and practical breakthrough in the field came in 1984 when Narendra Karmarkar introduced a new interior point method for solving linear programming problems.
Dantzig's original example of finding the best assignment of 70 people to 70 jobs exemplifies the usefulness of linear programming. The computing power required to test all the permutations to select the best assignment is vast; the number of possible configurations exceeds the number of particles in the universe. However, it takes only a moment to find the optimum solution by posing the problem as a linear program and applying the Simplex algorithm. The theory behind linear programming drastically reduces the number of possible optimal solutions that must be checked.
Uses
Linear programming is a considerable field of optimization for several reasons. Many practical problems in operations research can be expressed as linear programming problems. Certain special cases of linear programming, such as network flow problems and multicommodity flow problems are considered important enough to have generated much research on specialized algorithms for their solution. A number of algorithms for other types of optimization problems work by solving LP problems as sub-problems. Historically, ideas from linear programming have inspired many of the central concepts of optimization theory, such as duality, decomposition, and the importance of convexity and its generalizations. Likewise, linear programming is heavily used in microeconomics and company management, such as planning, production, transportation, technology and other issues. Although the modern management issues are ever-changing, most companies would like to maximize profits or minimize costs with limited resources. Therefore, many of issues can boil down to linear programming problems.
Standard form
Standard form is the usual and most intuitive form of describing a linear programming problem. It consists of the following three parts:
- A linear function to be maximized
- e.g. maximize

- Problem constraints of the following form
- e.g.

- Non-negative variables
- e.g.

The problem is usually expressed in matrix form, and then becomes:
- maximize

- subject to

Other forms, such as minimization problems, problems with constraints on alternative forms, as well as problems involving negative variables can always be rewritten into an equivalent problem in standard form.
Example
Suppose that a farmer has a piece of farm land, say A square kilometres large, to be planted with either wheat or barley or some combination of the two. The farmer has a limited permissible amount F of fertilizer and P of insecticide which can be used, each of which is required in different amounts per unit area for wheat (F1, P1) and barley (F2, P2). Let S1 be the selling price of wheat, and S2 the price of barley. If we denote the area planted with wheat and barley by x1 and x2 respectively, then the optimal number of square kilometres to plant with wheat vs barley can be expressed as a linear programming problem:
maximize  | (maximize the revenue — revenue is the "objective function") | |
| subject to |  | (limit on total area) |
 | (limit on fertilizer) | |
 | (limit on insecticide) | |
 | (cannot plant a negative area) | |
Which in matrix form becomes:
- maximize

- subject to

Augmented form (slack form)
Linear programming problems must be converted into augmented form before being solved by the simplex algorithm. This form introduces non-negative slack variables to replace inequalities with equalities in the constraints. The problem can then be written in the following form:
- Maximize Z in:


where  are the newly introduced slack variables, and Z is the variable to be maximized.
are the newly introduced slack variables, and Z is the variable to be maximized.
Example
The example above becomes as follows when converted into augmented form:
maximize  | (objective function) | |
| subject to |  | (augmented constraint) |
 | (augmented constraint) | |
 | (augmented constraint) | |
 | ||
where  are (non-negative) slack variables.
are (non-negative) slack variables.
Which in matrix form becomes:
- Maximize Z in:

Duality
Every linear programming problem, referred to as a primal problem, can be converted into a dual problem, which provides an upper bound to the optimal value of the primal problem. In matrix form, we can express the primal problem as:
- maximize

- subject to

The corresponding dual problem is:
- minimize

- subject to

where y is used instead of x as variable vector.
There are two ideas fundamental to duality theory. One is the fact that the dual of a dual linear program is the original primal linear program. Additionally, every feasible solution for a linear program gives a bound on the optimal value of the objective function of its dual. The weak duality theorem states that the objective function value of the dual at any feasible solution is always greater than or equal to the objective function value of the primal at any feasible solution. The strong duality theorem states that if the primal has an optimal solution, x*, then the dual also has an optimal solution, y*, such that cTx*=bTy*.
A linear program can also be unbounded or infeasible. Duality theory tells us that if the primal is unbounded then the dual is infeasible by the weak duality theorem. Likewise, if the dual is unbounded, then the primal must be infeasible. However, it is possible for both the dual and the primal to be infeasible (See also Farkas' lemma).
Example
Revisit the above example of the farmer who may grow wheat and barley with the set provision of some A land, F fertilizer and P insecticide. Assume now that unit prices for each of these means of production (inputs) are set by a planning board. The planning board's job is to minimize the total cost of procuring the set amounts of inputs while providing the farmer with a floor on the unit price of each of his crops (outputs), S1 for wheat and S2 for barley. This corresponds to the following linear programming problem:
minimize  | (minimize the total cost of the means of production as the "objective function") | |
| subject to |  | (the farmer must receive no less than S1 for his wheat) |
 | (the farmer must receive no less than S2 for his barley) | |
 | (prices cannot be negative) | |
Which in matrix form becomes:
- minimize

- subject to

The primal problem deals with physical quantities. With all inputs available in limited quantities, and assuming the unit prices of all outputs is known, what quantities of outputs to produce so as to maximize total revenue? The dual problem deals with economic values. With floor guarantees on all output unit prices, and assuming the available quantity of all inputs is known, what input unit pricing scheme to set so as to minimize total expenditure?
To each variable in the primal space corresponds an inequality to satisfy in the dual space, both indexed by output type. To each inequality to satisfy in the primal space corresponds a variable in the dual space, both indexed by input type.
The coefficients which bound the inequalities in the primal space are used to compute the objective in the dual space, input quantities in this example. The coefficients used to compute the objective in the primal space bound the inequalities in the dual space, output unit prices in this example.
Both the primal and the dual problems make use of the same matrix. In the primal space, this matrix expresses the consumption of physical quantities of inputs necessary to produce set quantities of outputs. In the dual space, it expresses the creation of the economic values associated with the outputs from set input unit prices.
Since each inequality can be replaced by an equality and a slack variable, this means each primal variable corresponds to a dual slack variable, and each dual variable corresponds to a primal slack variable. This relation allows us to complementary slackness.
Special cases
A packing LP is a linear program of the form
- maximize

- subject to

such that the matrix  and the vectors
and the vectors  and
and  are non-negative.
are non-negative.
The dual of a packing LP is a covering LP, a linear program of the form
- minimize

- subject to

such that the matrix  and the vectors
and the vectors  and
and  are non-negative.
are non-negative.
Examples
Covering and packing LPs commonly arise as a
Finding a fractional coloring of a graph is another example of a covering LP. In this case, there is one constraint for each vertex of the graph and one variable for each independent set of the graph.
Complementary slackness
It is possible to obtain an optimal solution to the dual when only an optimal solution to the primal is known using the complementary slackness theorem. The theorem states:
Suppose that x = (x1, x2, . . ., xn) is primal feasible and that y = (y1, y2, . . . , ym) is dual feasible. Let (w1, w2, . . ., wm) denote the corresponding primal slack variables, and let (z1, z2, . . . , zn) denote the corresponding dual slack variables. Then x and y are optimal for their respective problems if and only if xjzj = 0, for j = 1, 2, . . . , n, wiyi = 0, for i = 1, 2, . . . , m.
So if the ith slack variable of the primal is not zero, then the ith variable of the dual is equal zero. Likewise, if the jth slack variable of the dual is not zero, then the jth variable of the primal is equal to zero.
Theory
Geometrically, the linear constraints define a convex polyhedron, which is called the feasible region. Since the objective function is also linear, hence a convex function, all local optima are automatically global optima (by the
There are two situations in which no optimal solution can be found. First, if the constraints contradict each other (for instance, x ≥ 2 and x ≤ 1) then the feasible region is empty and there can be no optimal solution, since there are no solutions at all. In this case, the LP is said to be infeasible.
Alternatively, the polyhedron can be unbounded in the direction of the objective function (for example: maximize x1 + 3 x2 subject to x1 ≥ 0, x2 ≥ 0, x1 + x2 ≥ 10), in which case there is no optimal solution since solutions with arbitrarily high values of the objective function can be constructed.
Barring these two pathological conditions (which are often ruled out by resource constraints integral to the problem being represented, as above), the optimum is always attained at a vertex of the polyhedron. However, the optimum is not necessarily unique: it is possible to have a set of optimal solutions covering an edge or face of the polyhedron, or even the entire polyhedron (This last situation would occur if the objective function were constant).
Algorithms

The simplex algorithm, developed by George Dantzig, solves LP problems by constructing an admissible solution at a vertex of the polyhedron and then walking along edges of the polyhedron to vertices with successively higher values of the objective function until the optimum is reached. Although this algorithm is quite efficient in practice and can be guaranteed to find the global optimum if certain precautions against cycling are taken, it has poor worst-case behavior: it is possible to construct a linear programming problem for which the simplex method takes a number of steps exponential in the problem size. In fact, for some time it was not known whether the linear programming problem was solvable in polynomial time (complexity class P).
This long standing issue was resolved by Leonid Khachiyan in 1979 with the introduction of the ellipsoid method, the first worst-case polynomial-time algorithm for linear programming. To solve a problem which has n variables and can be encoded in L input bits, this algorithm uses O(n4L) arithmetic operations on numbers with O(L) digits. It consists of a specialization of the nonlinear optimization technique developed by Naum Z. Shor, generalizing the ellipsoid method for convex optimization proposed by Arkadi Nemirovski, a 2003 John von Neumann Theory Prize winner, and D. Yudin.
Khachiyan's algorithm was of landmark importance for establishing the polynomial-time solvability of linear programs. The algorithm had little practical impact, as the simplex method is more efficient for all but specially constructed families of linear programs. However, it inspired new lines of research in linear programming with the development of interior point methods, which can be implemented as a practical tool. In contrast to the simplex algorithm, which finds the optimal solution by progresses along points on the boundary of a polyhedral set, interior point methods move through the interior of the feasible region.
In 1984, N. Karmarkar proposed a new interior point projective method for linear programming. Karmarkar's algorithm not only improved on Khachiyan's theoretical worst-case polynomial bound (giving O(n3.5L)), but also promised dramatic practical performance improvements over the simplex method. Since then, many interior point methods have been proposed and analyzed. Early successful implementations were based on affine scaling variants of the method. For both theoretical and practical properties, barrier function or path-following methods are the most common recently.
The current opinion is that the efficiency of good implementations of simplex-based methods and interior point methods is similar for routine applications of linear programming.
LP solvers are in widespread use for optimization of various problems in industry, such as optimization of flow in transportation networks, many of which can be transformed into linear programming problems only with some difficulty.
Open problems and recent work
There are several open problems in the theory of linear programming, the solution of which would represent fundamental breakthroughs in mathematics and potentially major advances in our ability to solve large-scale linear programs.
- Does LP admit a strongly polynomial-time algorithm?
- Does LP admit a strongly polynomial algorithm to find a strictly complementary solution?
- Does LP admit a polynomial algorithm in the real number (unit cost) model of computation?
This closely related set of problems has been cited by Stephen Smale as among the 18 greatest unsolved problems of the 21st century. In Smale's words, the third version of the problem "is the main unsolved problem of linear programming theory." While algorithms exist to solve linear programming in weakly polynomial time, such as the ellipsoid methods and interior-point techniques, no algorithms have yet been found that allow strongly polynomial-time performance in the number of constraints and the number of variables. The development of such algorithms would be of great theoretical interest, and perhaps allow practical gains in solving large LPs as well.
- Are there pivot rules which lead to polynomial-time Simplex variants?
- Do all polyhedral graphs have polynomially-bounded diameter?
- Is the Hirsch conjecture true for polyhedral graphs?
These questions relate to the performance analysis and development of Simplex-like methods. The immense efficiency of the Simplex algorithm in practice despite its exponential-time theoretical performance hints that there may be variations of Simplex that run in polynomial or even strongly polynomial time. It would be of great practical and theoretical significance to know whether any such variants exist, particularly as an approach to deciding if LP can be solved in strongly polynomial time.
The Simplex algorithm and its variants fall in the family of edge-following algorithms, so named because they solve linear programming problems by moving from vertex to vertex along edges of a polyhedron. This means that their theoretical performance is limited by the maximum number of edges between any two vertices on the LP polyhedron. As a result, we are interested in knowing the maximum graph-theoretical diameter of polyhedral graphs. It has been proved that all polyhedra have subexponential diameter, and all experimentally observed polyhedra have linear diameter, it is presently unknown whether any polyhedron has superpolynomial or even superlinear diameter. If any such polyhedra exist, then no edge-following variant can run in polynomial or linear time, respectively. Questions about polyhedron diameter are of independent mathematical interest.
Simplex pivot methods preserve primal (or dual) feasibility. On the other hand, criss-cross pivot methods do not preserve (primal or dual) feasibility --- they may visit primal feasible, dual feasible or primal-and-dual infeasible bases in any order. Pivot methods of this type have been studied since the 1970s. Essentially, these methods attempt to find the shortest pivot path on the arrangement polytope under the linear programming problem. In contrast to polyhedral graphs, graphs of arrangement polytopes have small diameter, allowing the possibility of strongly polynomial-time criss-cross pivot method without resolving questions about the diameter of general polyhedra.
Integer unknowns
If the unknown variables are all required to be integers, then the problem is called an integer programming (IP) or integer linear programming (ILP) problem. In contrast to linear programming, which can be solved efficiently in the worst case, integer programming problems are in many practical situations (those with bounded variables) NP-hard. 0-1 integer programming or binary integer programming (BIP) is the special case of integer programming where variables are required to be 0 or 1 (rather than arbitrary integers). This problem is also classified as NP-hard, and in fact the decision version was one of Karp's 21 NP-complete problems.
If only some of the unknown variables are required to be integers, then the problem is called a mixed integer programming (MIP) problem. These are generally also NP-hard.
There are however some important subclasses of IP and MIP problems that are efficiently solvable, most notably problems where the constraint matrix is totally unimodular and the right-hand sides of the constraints are integers.
Advanced algorithms for solving integer linear programs include:
- cutting-plane method
- branch and bound
- branch and cut
- branch and price
- if the problem has some extra structure, it may be possible to apply delayed column generation.
OR-Notes
J E Beasley
OR-Notes are a series of introductory notes on topics that fall under the broad heading of the field of operations research (OR). They were originally used by me in an introductory OR course I give at Imperial College. They are now available for use by any students and teachers interested in OR subject to the following conditions.
A full list of the topics available in OR-Notes can be found here.
Linear programming - formulation
You will recall from the Two Mines example that the conditions for a mathematical model to be a linear program (LP) were:
- all variables continuous (i.e. can take fractional values)
- a single objective (minimise or maximise)
- the objective and constraints are linear i.e. any term is either a constant or a constant multiplied by an unknown.
LP's are important - this is because:
- many practical problems can be formulated as LP's
- there exists an algorithm (called the simplex algorithm) which enables us to solve LP's numerically relatively easily.
We will return later to the simplex algorithm for solving LP's but for the moment we will concentrate upon formulating LP's.
Some of the major application areas to which LP can be applied are:
- Blending
- Production planning
- Oil refinery management
- Distribution
- Financial and economic planning
- Manpower planning
- Blast furnace burdening
- Farm planning
We consider below some specific examples of the types of problem that can be formulated as LP's. Note here that the key to formulating LP's is practice. However a useful hint is that common objectives for LP's are minimise cost/maximise profit.
Financial planning
A bank makes four kinds of loans to its personal customers and these loans yield the following annual interest rates to the bank:
- First mortgage 14%
- Second mortgage 20%
- Home improvement 20%
- Personal overdraft 10%
The bank has a maximum foreseeable lending capability of £250 million and is further constrained by the policies:
- first mortgages must be at least 55% of all mortgages issued and at least 25% of all loans issued (in £ terms)
- second mortgages cannot exceed 25% of all loans issued (in £ terms)
- to avoid public displeasure and the introduction of a new windfall tax the average interest rate on all loans must not exceed 15%.
Formulate the bank's loan problem as an LP so as to maximise interest income whilst satisfying the policy limitations.
Note here that these policy conditions, whilst potentially limiting the profit that the bank can make, also limit its exposure to risk in a particular area. It is a fundamental principle of risk reduction that risk is reduced by spreading money (appropriately) across different areas.
Financial planning solution
We follow the same approach as for the Two Mines example - namely
- variables
- constraints
- objective.
Note here that as in all formulation exercises we are translating a verbal description of the problem into an equivalent mathematical description.
A useful tip when formulating LP's is to express the variables, constraints and objective in words before attempting to express them in mathematics.
Variables
Essentially we are interested in the amount (in £) the bank has loaned to customers in each of the four different areas (not in the actual number of such loans). Hence let
xi = amount loaned in area i in £m (where i=1 corresponds to first mortgages, i=2 to second mortgages etc)
and note that xi >= 0 (i=1,2,3,4).
Note here that it is conventional in LP's to have all variables >= 0. Any variable (X, say) which can be positive or negative can be written as X1-X2 (the difference of two new variables) where X1 >= 0 and X2 >= 0.
Constraints
(a) limit on amount lent
x1 + x2 + x3 + x4 <= 250
Note here the use of <= rather than = (following the general rule we put forward in the Two Mines problem, namely given a choice between an equality and an inequality choose the inequality (as this allows for more flexibility in optimising the objective function)).
(b) policy condition 1
x1 >= 0.55(x1 + x2)
i.e. first mortgages >= 0.55(total mortgage lending) and also
x1 >= 0.25(x1 + x2 + x3 + x4)
i.e. first mortgages >= 0.25(total loans)
(c) policy condition 2
x2 <= 0.25(x1 + x2 + x3 + x4)
(d) policy condition 3 - we know that the total annual interest is 0.14x1 + 0.20x2 + 0.20x3 + 0.10x4 on total loans of (x1 + x2 + x3 + x4). Hence the constraint relating to policy condition (3) is
0.14x1 + 0.20x2 + 0.20x3 + 0.10x4 <= 0.15(x1 + x2 + x3 + x4)
Note: whilst many of the constraints given above could be simplified by collecting together terms this is not strictly necessary until we come to solve the problem numerically and does tend to obscure the meaning of the constraints.
Objective
To maximise interest income (which is given above) i.e.
maximise 0.14x1 + 0.20x2 + 0.20x3 + 0.10x4
In case you are interested the optimal solution to this LP (solved using the package as dealt with later) is x1= 208.33, x2=41.67 and x3=x4=0. Note here this this optimal solution is not unique - other variable values, e.g. x1= 62.50, x2=0, x3=100 and x4=87.50 also satisfy all the constraints and have exactly the same (maximum) solution value of 37.5
Blending problem
Consider the example of a manufacturer of animal feed who is producing feed mix for dairy cattle. In our simple example the feed mix contains two active ingredients and a filler to provide bulk. One kg of feed mix must contain a minimum quantity of each of four nutrients as below:
Nutrient A B C D
gram 90 50 20 2
The ingredients have the following nutrient values and cost
A B C D Cost/kg
Ingredient 1 (gram/kg) 100 80 40 10 40
Ingredient 2 (gram/kg) 200 150 20 - 60
What should be the amounts of active ingredients and filler in one kg of feed mix?
Blending problem solution
Variables
In order to solve this problem it is best to think in terms of one kilogram of feed mix. That kilogram is made up of three parts - ingredient 1, ingredient 2 and filler so let:
x1 = amount (kg) of ingredient 1 in one kg of feed mix
x2 = amount (kg) of ingredient 2 in one kg of feed mix
x3 = amount (kg) of filler in one kg of feed mix
where x1 >= 0, x2 >= 0 and x3 >= 0.
Essentially these variables (x1, x2 and x3) can be thought of as the recipe telling us how to make up one kilogram of feed mix.
Constraints
- nutrient constraints
100x1 + 200x2 >= 90 (nutrient A)
80x1 + 150x2 >= 50 (nutrient B)
40x1 + 20x2 >= 20 (nutrient C)
10x1 >= 2 (nutrient D)
Note the use of an inequality rather than an equality in these constraints, following the rule we put forward in the Two Mines example, where we assume that the nutrient levels we want are lower limits on the amount of nutrient in one kg of feed mix.
- balancing constraint (an implicit constraint due to the definition of the variables)
x1 + x2 + x3 = 1
Objective
Presumably to minimise cost, i.e.
minimise 40x1 + 60x2
which gives us our complete LP model for the blending problem.
In case you are interested the optimal solution to this LP (solved using the package as dealt with later) is x1= 0.3667, x2=0.2667 and x3=0.3667 to four decimal places.
Obvious extensions/uses for this LP model include:
- increasing the number of nutrients considered
- increasing the number of possible ingredients considered - more ingredients can never increase the overall cost (other things being unchanged), and may lead to a decrease in overall cost
- placing both upper and lower limits on nutrients
- dealing with cost changes
- dealing with supply difficulties
- filler cost
Blending problems of this type were, in fact, some of the earliest applications of LP (for human nutrition during rationing) and are still widely used in the production of animal feedstuffs.
Production planning problem
A company manufactures four variants of the same product and in the final part of the manufacturing process there are assembly, polishing and packing operations. For each variant the time required for these operations is shown below (in minutes) as is the profit per unit sold.
Assembly Polish Pack Profit (£)
Variant 1 2 3 2 1.50
2 4 2 3 2.50
3 3 3 2 3.00
4 7 4 5 4.50
- Given the current state of the labour force the company estimate that, each year, they have 100000 minutes of assembly time, 50000 minutes of polishing time and 60000 minutes of packing time available. How many of each variant should the company make per year and what is the associated profit?
- Suppose now that the company is free to decide how much time to devote to each of the three operations (assembly, polishing and packing) within the total allowable time of 210000 (= 100000 + 50000 + 60000) minutes. How many of each variant should the company make per year and what is the associated profit?
Production planning solution
Variables
Let:
xi be the number of units of variant i (i=1,2,3,4) made per year
Tass be the number of minutes used in assembly per year
Tpol be the number of minutes used in polishing per year
Tpac be the number of minutes used in packing per year
where xi >= 0 i=1,2,3,4 and Tass, Tpol, Tpac >= 0
Constraints
(a) operation time definition
Tass = 2x1 + 4x2 + 3x3 + 7x4 (assembly)
Tpol = 3x1 + 2x2 + 3x3 + 4x4 (polish)
Tpac = 2x1 + 3x2 + 2x3 + 5x4 (pack)
(b) operation time limits
The operation time limits depend upon the situation being considered. In the first situation, where the maximum time that can be spent on each operation is specified, we simply have:
Tass <= 100000 (assembly)
Tpol <= 50000 (polish)
Tpac <= 60000 (pack)
In the second situation, where the only limitation is on the total time spent on all operations, we simply have:
Tass + Tpol + Tpac <= 210000 (total time)
Objective
Presumably to maximise profit - hence we have
maximise 1.5x1 + 2.5x2 + 3.0x3 + 4.5x4
which gives us the complete formulation of the problem.
We shall solve this particular problem later in the course.
Factory planning problem
Under normal working conditions a factory produces up to 100 units of a certain product in each of four consecutive time periods at costs which vary from period to period as shown in the table below.
Additional units can be produced by overtime working. The maximum quantity and costs are shown in the table below, together with the forecast demands for the product in each of the four time periods.
Time Demand Normal Overtime Overtime
Period (units) Production Production Production
Costs Capacity Cost
(£K/unit) (units) (£K/unit)
1 130 6 60 8
2 80 4 65 6
3 125 8 70 10
4 195 9 60 11
It is possible to hold up to 70 units of product in store from one period to the next at a cost of £1.5K per unit per period. (This figure of £1.5K per unit per period is known as a stock-holding cost and represents the fact that we are incurring costs associated with the storage of stock).
It is required to determine the production and storage schedule which will meet the stated demands over the four time periods at minimum cost given that at the start of period 1 we have 15 units in stock. Formulate this problem as an LP.
Factory planning solution
Variables
The decisions that need to be made relate to the amount to produce in normal/overtime working each period. Hence let:
xt = number of units produced by normal working in period t (t=1,2,3,4), where xt >= 0
yt = number of units produced by overtime working in period t (t=1,2,3,4) where yt >= 0
In fact, for this problem, we also need to decide how much stock we carry over from one period to the next so let:
It = number of units in stock at the end of period t (t=0,1,2,3,4)
Constraints
- production limits
xt <= 100 t=1,2,3,4
y1 <= 60
y2 <= 65
y3 <= 70
y4 <= 60
- limit on space for stock carried over
It <= 70 t=1,2,3,4
- we have an inventory continuity equation of the form
closing stock = opening stock + production - demand
then assuming
- opening stock in period t = closing stock in period t-1 and
- that production in period t is available to meet demand in period t
we have that
I1 = I0 + (x1 + y1) - 130
I2 = I1 + (x2 + y2) - 80
I3 = I2 + (x3 + y3) - 125
I4 = I3 + (x4 + y4) - 195
where I0 = 15
Note here that inventory continuity equations of the type shown above are common in production planning problems involving more than one time period. Essentially the inventory variables (It) and the inventory continuity equations link together the time periods being considered and represent a physical accounting for stock.
- demand must always be met - i.e. no "stock-outs". This is equivalent to saying that the opening stock in period t plus the production in period t must be greater than (or equal to) the demand in period t, i.e.
I0 + (x1 + y1) >= 130
I1 + (x2 + y2) >= 80
I2 + (x3 + y3) >= 125
I3 + (x4 + y4) >= 195
However these equations can be viewed in another way. Considering the inventory continuity equations we have that the above equations which ensure that demand is always met can be rewritten as:
I1 >= 0
I2 >= 0
I3 >= 0
I4 >= 0
Objective
To minimise cost - which consists of the cost of ordinary working plus the cost of overtime working plus the cost of carrying stock over (1.5K per unit). Hence the objective is:
minimise
(6x1 + 4x2 + 8x3 + 9x4) + (8y1 + 6y2 + 10y3 + 11y4) + (1.5I0 + 1.5I1 + 1.5I2 + 1.5I3 + 1.5I4)
Note here that we have assumed that if we get an answer involving fractional variable values this is acceptable (since the number of units required each period is reasonably large this should not cause too many problems).
In case you are interested the optimal solution to this LP (solved using the package as dealt with later) is x1=x2=x3=x4=100; y1=15, y2=50, y3=0 and y4=50; I0=15, I1=0, I2=70, I3=45 and I4=0 with the minimal objective function value being 3865
Note:
- As discussed above assuming It >= 0 t=1,2,3,4 means "no stock-outs" i.e. we need a production plan in which sufficient is produced to ensure that demand is always satisfied.
- Allowing It (t=1,2,3,4) to be unrestricted (positive or negative) means that we may end up with a production plan in which demand is unsatisfied in period t (It <>
- If It is allowed to be negative then we need to amend the objective to ensure that we correctly account for stock-holding costs (and possibly to account for stock-out costs).
- If we get a physical loss of stock over time (e.g. due to damage, pilferage, etc) then this can be easily accounted for. For example if we lose (on average) 2% of stock each period then multiply the right-hand side of the inventory continuity equation by 0.98. If this is done then we often include a term in the objective function to account financially for the loss of stock.
- If production is not immediately available to meet customer demand then the appropriate time delay can be easily incorporated into the inventory continuity equation. For example a 2 period time delay for the problem dealt with above means replace (xt + yt) in the inventory continuity equation for It by (xt-2 + yt-2).
- In practice we would probably deal with the situation described above on a "rolling horizon" basis in that we would get an initial production plan based on current data and then, after one time period (say), we would update our LP and resolve to get a revised production plan. In other words even though we plan for a specific time horizon, here 4 months, we would only even implement the plan for the first month, so that we are always adjusting our 4 month plan to take account of future conditions as our view of the future changes. We illustrate this below.
Period 1 2 3 4 5 6 7 8 P=plan
P P P P D=do (follow) the plan in a period
D P P P P
D P P P P
D P P P P
This rolling horizon approach would be preferable to carrying out the plan for 4 time periods and then producing a new plan for the next 4 time periods, such as shown below.
Period 1 2 3 4 5 6 7 8 P=plan
P P P P D=do (follow) the plan in a period
D D D D
P P P P
D D D D
Some more LP formulation examples can be found here.
The holdout sample results indicate that the MP function had a "hit rate" for failed firms equal to 73.1%, whereas this rate for the logit function was equal to 66.7%. For non-failed firms, the "hit rates" were 75.4% and 74.4%, respectively. Thus, this test can be said to support the hypothesis that mathematical programming performs at least as well as logistic regression. In fact, the test results showed that the former even performed better than the latter, but one test cannot provide conclusive evidence as regards the superiority of the former method. Overall, the predictive ability of both models was rather poor, but this is not surprising considering that the task was to predict bankruptcy within three years or less.
It is interesting to note that the logit model performed considerably better than the MP model when applied to the estimation sample. Obviously, the logit estimation procedure provides a "tighter" model of the data than the MP procedure, but this can lead to diminished predictive ability if, as in this case, the failure rate increases and the raw scores of key financial ratios deteriorate as a result of recession, resulting in considerable differences between the estimation and holdout samples.
Summary
The purpose of this study has been to test whether mathematical programming performs as well as logistic regression when the task is to predict bankruptcy. In the empirical test carried out here on a large holdout sample (78 failed firms, 922 non-failed firms), the mathematical programming function performed better than the logit model both for failed firms and for non-failed firms, confirming our hypothesis that mathematical programming performs at least as well as logistic regression in terms of ability to predict bankruptcy.




No comments:
Post a Comment